ผู้เขียน: Site Editor ที่มา: สถานที่
เมื่อเปรียบเทียบกับรูปร่างอื่น ๆ ของเลนส์แสง เลนส์พระจันทร์โค้งมักไม่มีให้เป็นผลิตภัณฑ์สำเร็จรูป เลนส์พระจันทร์โค้งใช้หลักในการโฟกัสจุดเล็ก ๆ หรือการปรับแสงให้ขนาน ในขณะที่เลนส์พลาโน-คอนเวกซ์มักจะเสนออัตราส่วนราคา/ประสิทธิภาพที่ดีกว่า อย่างไรก็ตาม มีบางกรณีที่เลนส์พระจันทร์โค้งมอบประสิทธิภาพที่เหนือกว่าในราคาที่สูงขึ้นเล็กน้อย
ความผิดเพี้ยนแบบทรงกลม
เนื่องจากลักษณะทรงกลมของเลนส์ การบิดเบือนแบบทรงกลมจะทำให้ลำแสงขนานกันจากแกนแสงอยู่ที่ระยะต่างๆ โดยไม่บรรจบกันที่จุดเดียวกัน (รูปที่ 1) แม้ว่าจะสามารถใช้เลนส์หลายชิ้นเพื่อแก้ไขการบิดเบือนแบบทรงกลมได้ แต่สำหรับระบบอินฟราเรดหลายระบบซึ่งต้นทุนของวัสดุมีราคาสูงกว่าวัสดุในช่วงคลื่นมองเห็นมาก จึงเป็นที่ต้องการที่จะลดจำนวนของเลนส์ การบิดเบือนแบบทรงกลมของเลนส์เดี่ยวสามารถลดลงได้โดยการสร้างรูปร่างของเลนส์ให้เหมาะสมที่สุด
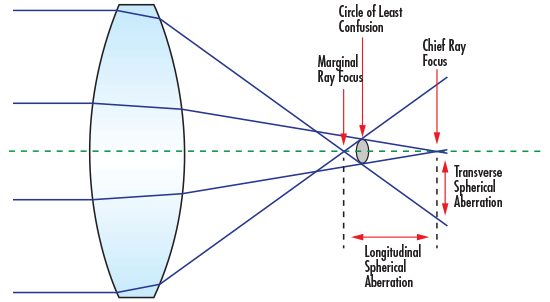
รูปที่ 1: การบิดเบือนแบบทรงกลม
สำหรับดัชนีหักเหและความหนาของเลนส์ที่คงที่ จะมีจำนวนรวมของรัศมีที่เป็นไปได้ไม่จำกัด ซึ่งสามารถนำมาใช้ในการสร้างเลนส์ที่มีระยะโฟกัสเฉพาะเหล่านี้ รัศมีเหล่านี้จะสร้างรูปร่างเลนส์ที่แตกต่างกัน ซึ่งส่งผลโดยตรงต่อการบิดเบือนแบบทรงกลมและการบิดเบือนแบบคอม่าเนื่องจากการโค้งของแสงขณะผ่านเลนส์
รูปร่างของเลนส์สามารถอธิบายได้ด้วยปัจจัย Coddington shape factor C (สมการที่ 1 และรูปที่ 2)

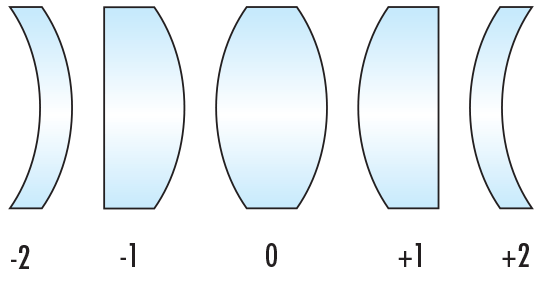
รูปที่ 2: ตัวประกอบรูปร่างของ Coddington สำหรับการจัดเรียงเลนส์ที่แตกต่างกัน
โดยใช้สมการความผิดเพี้ยนของเลนส์บาง (ใช้วัตถุที่อนันต์และตำแหน่งของเลนส์หยุด) เราสามารถอนุมานเงื่อนไขที่สร้างความผิดเพี้ยนทรงกลมขั้นต่ำได้ (สมการที่ 2)
หากสมมติว่าความยาวคลื่นคงที่สามารถรักษาไว้ได้ ความสัมพันธ์ระหว่างเลขชี้กำลังและตัวประกอบรูปร่างที่สร้างความผิดเพี้ยนทรงกลมขั้นต่ำสามารถแสดงผลได้ (รูปที่ 3)

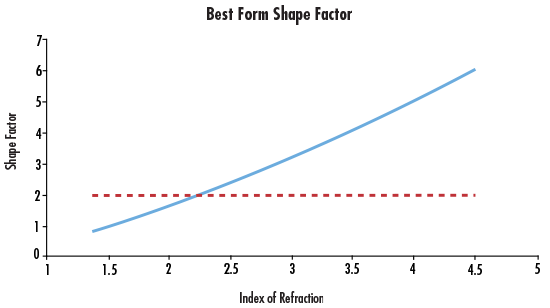
รูปที่ 3: ตัวประกอบรูปร่างที่เหมาะสมตามดัชนีหักเหแสง
ประโยชน์ของการออกแบบแบบ curved moon
เมื่อทำงานในสภาพแวดล้อมที่มองเห็นได้ ดัชนีแก้วมักจะอยู่ระหว่าง 1.5 ถึง 1.7 และรูปร่างของความผิดเพี้ยนทรงกลมขั้นต่ำมักจะเป็น plano-convex เกือบทั้งหมด แต่ในสภาพแวดล้อมอินฟราเรด มักใช้วัสดุดัชนีสูง เช่น เยอรมานีียม เยอรมานีียม ซึ่งมีค่าสเปก 4.0 มอบประโยชน์อย่างมากจากการออกแบบเลนส์ curved-moon โดยลดความผิดเพี้ยนทรงกลมลงอย่างมาก
การเกิดความผิดเพี้ยนแบบทรงกลมขั้นต่ำเกิดขึ้นเมื่อแสงหักเหอย่างสม่ำเสมอที่ทั้งสองพื้นผิว แม้ว่าพื้นผิวด้านแรกของเลนส์รูปพระจันทร์จากสารเจิร์เมเนียมจะหักเหแสงมากกว่าเลนส์ PCX ที่คล้ายกันเล็กน้อย แต่พื้นผิวด้านหลังของเลนส์ PCX จะทำให้แสงหักเหมากขึ้น ส่งผลให้เกิดความผิดเพี้ยนแบบทรงกลมเพิ่มขึ้นโดยรวม
ตามที่แสดงในรูปที่ 4 ซึ่งเปรียบเทียบประสิทธิภาพของเลนส์ PCX เจิร์เมเนียมขนาด 25 x 25 มม. กับเลนส์รูปพระจันทร์เจิร์เมเนียมขนาด 25 x 25 มม. จะเห็นได้ง่ายว่าเลนส์ PCX หักเหแสงมากกว่าเมื่อเทียบกับพื้นผิวของเลนส์เมื่อเทียบกับเลนส์รูปพระจันทร์ การเพิ่มขึ้นของความโค้งส่งผลให้เกิดความผิดเพี้ยนแบบทรงกลมมากขึ้น เลนส์รูปพระจันทร์เจิร์เมเนียมแสดงถึงการลดลงอย่างมากของขนาดจุด ทำให้มันเหมาะสมสำหรับการใช้งานอินฟราเรดที่ต้องการความแม่นยำมากขึ้น

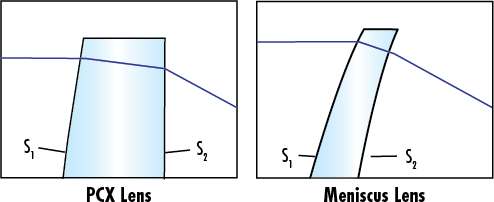
รูปที่ 4x: แผนภาพของเลนส์ PCX เจิร์เมเนียมขนาด 25 x 25 มม. VS เลนส์รูปพระจันทร์โค้งเจิร์เมเนียมขนาด 25 x 25 มม.
| เลนส์แบนเว้า | เลนส์รูปพระจันทร์ | |
| S1 ความผิดเพี้ยนแบบทรงกลม | 0.1 คลื่น | 2.4 คลื่น |
| S2 ความผิดเพี้ยนแบบทรงกลม | คลื่น 14.2 | คลื่น 2.9 |
| ความผิดเพี้ยนแบบทรงกลมทั้งหมด | คลื่น 14.3 | คลื่น 5.3 |
| ขนาดของจุด | 258μm | 83μm |
แม้ว่าเลนส์รูปพระจันทร์เสี้ยวจะยังคงให้ประสิทธิภาพสูงกว่าในช่วงแสงที่มองเห็นได้ แต่โดยปกติแล้วไม่มีการเพิ่มประสิทธิภาพมากพอที่จะชดเชยต้นทุนการผลิตที่เพิ่มขึ้น รูปที่ 1 แสดงการเปรียบเทียบประสิทธิภาพของเลนส์ PCX แคลเซียมฟลูออไรด์ (CaF2) ขนาด 25 x 50 มม. กับเลนส์รูปพระจันทร์เสี้ยวในแอปพลิเคชันสเปกตรัมแสงที่มองเห็นได้ และเลนส์ PCX เยอรมานี (Ge) ขนาด 25 x 50 มม. กับเลนส์รูปพระจันทร์เสี้ยวในแอปพลิเคชันช่วงอินฟราเรด ขนาดจุดโฟกัสของเลนส์เยอรมานีลดลงอย่างมากเมื่อใช้รูปร่างแบบเสี้ยวพระจันทร์
| ขนาดจุดโฟกัสของเลนส์เว้าโค้ง | ขนาดจุดโฟกัสของเลนส์พระจันทร์เสี้ยว | ขนาดของจุด | ลดลงโดยเลนส์พระจันทร์โค้ง |
| สเปกตรัมที่มองเห็นได้ (เลนส์ CaF2) | 849.3μm | 624.9μm | -26% |
| สเปกโตรโฟโตเมตรีอินฟราเรด (เลนส์ Ge) | 258μm | 83μm | -68% |
ตารางที่ 1: การเปรียบเทียบขนาดจุดระหว่างเลนส์พลาโน-คอนเวกซ์และเลนส์พระจันทร์โค้งสำหรับการใช้งานในช่วงคลื่นที่มองเห็นได้และอินฟราเรด
แม้ว่าเลนส์พระจันทร์โค้งอาจไม่ให้ประโยชน์ในทุกการใช้งาน แต่พวกมันสามารถมอบข้อได้เปรียบด้านต้นทุนและประสิทธิภาพอย่างมากสำหรับการใช้งานอินฟราเรดหลายประเภท เช่น สเปกโตรโฟโตเมตรี
 ข่าวร้อน
ข่าวร้อน2023-06-06
2023-08-12
2023-08-19
2023-08-26